9 сентября, 2014
Андрей Антонов 
Датчики играют в робототехнике одну из важнейших ролей. При помощи различных датчиков робот «чувствует» себя самого и окружающий мир. Это органы чувств — глаза, уши, кожа для роботов.
Сенсорами часто называют более узкий класс измерителей - бесконтактные датчики, но зачастую термины датчик и сенсор используются просто как синонимы.
Возьмем определение:
Датчик, сенсор (от англ. sensor) — термин систем управления, первичный преобразователь, элемент измерительного, сигнального, регулирующего или управляющего устройства системы, преобразующий контролируемую величину в удобный для использования сигнал.
Оценка движения при помощи датчиков
Давайте проведем эксперимент.
Движение робота по квадратному пути
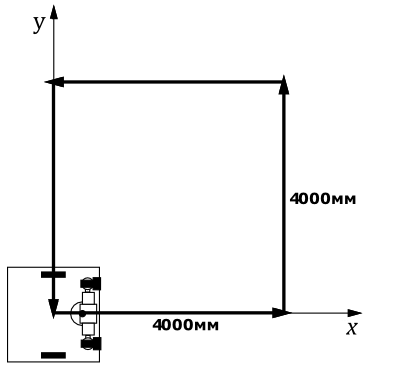
Возьмем небольшого мобильного робота (например, робот-пылесос) и поставим перед ним задачу: необходимо пройти путь, повторяющий квадрат со стороной 4 метра и вернуться в исходную точку. Насколько хорошо мы сможем оценивать движение робота, используя данные одометрии, которые мы получаем с колесных датчиков?
Картина, которую мы увидим, скорее всего, будет выглядеть примерно следующим образом:
Занос робота от идеальной траектории движения
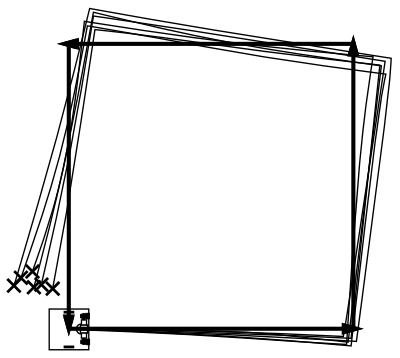
Робота будет, как будто, «заносить». Причиной такого поведения могут являться:
- ошибка начального выравнивания относительно осей в неподвижной системе координат (мы изначально поставили робота «криво»);
- пробуксовка колес;
- некорректная калибровка;
- отличия между реальными характеристиками левого и правого моторов;
- другие факторы.
Конечно, если будем использовать моторные энкодеры, которые обладают высокой точностью и синхронизируем оба мотора, то ситуация, наверное, улучшится, но, многократно повторяя свой эксперимент, мы не сможем каждый раз получать идеальную траекторию движения.
После проведения тщательной калибровки, попытавшись, тем самым учесть отличия характеристик реального устройства от теоретических параметров, мы увидим, что робот, в среднем, возвращается в исходную точку, но разброс все еще имеется. Мы не смогли исключить неконтроллируемые нами факторы (переменную пробуксовку колес, неравномерность свойств поверхности, по которой движется робот, даже потоки воздуха влияют!). Проведя калибровку, мы устранили систематическую ошибку, но все еще осталась ошибка с нулевым средним.
Устранена систематическая ошибка
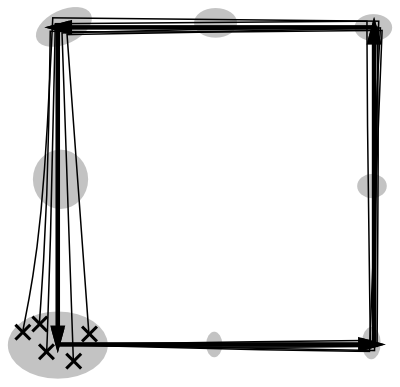
Для таких случайных ошибок мы можем построить вероятностную модель. В качестве модели в реальных физических системах хорошо подходит нормальное распределение (или как его еще называют — распределение Гаусса).
Чем дальше робот двигаться вдоль пути, тем сильнее реальное положение робота будет отклоняться в ту или иную сторону от идеальной траектории — дисперсия ошибки будет увеличиваться. Вследствие этого, провести точное интегрирование движения нашего робота, используя данные одометрии невозможно.
Реальная модель движения робота должна учитывать, что траектория, по которой двигается робот зависит от неопределенных помех, присутствует «шум движения». Для учета этого шума, уравнения, которые я приводил в предыдущей статье, перепишем
для прямолинейного движения на расстояние 
в виде
![\[ \left(\begin{array}{c}x_{new} \\ y_{new} \\ \theta_{new} \end{array}\right) = \left(\begin{array}{c}x + (D + e) \cos \theta\\ y + (D + e) \sin \theta \\ \theta + f \end{array}\right) \]](https://quicklatex.com/cache3/c6/ql_36099a86c00c617ed4477e8e4623bbc6_l3.png "Rendered by QuickLaTeX.com")
и для вращательного движения с поворотом на угол 
![\[ \left(\begin{array}{c}x_{new} \\ y_{new} \\ \theta_{new} \end{array}\right) = \left(\begin{array}{c}x \\ y \\ \theta + \alpha \end{array}\right) \]](https://quicklatex.com/cache3/25/ql_877f8e1a80a78ebf0e0265c3ab436925_l3.png "Rendered by QuickLaTeX.com")
В этих уравнениях — 
, 
и 
— шумовые составляющие с нормальным распределением, которые имеют нулевое среднее. Эти компоненты описывают, насколько реальное движение может отличаться от движения по идеальной траектории. Добавив шумовые составляющие в уравнения, мы не поможем роботу двигаться точнее, но они станут важны позже, когда мы объедимим одометрию с другими измерениями, используя вероятностный подход.
Проприоцептивные датчики
Проприоцептивные датчики — это сенсоры, которые показывают внутреннее состояние системы. В качестве примеров, можно привести моторные энкодеры, а также датчики силовых воздействий. Этот тип датчиков предназначен для улучшения восприятия роботом собственного внутреннего состояния, а также производимого движения.
Все датчики собирают некоторые числовые показания, или, как говорят измерения.
Для проприоцептивных датчиков, измеренное значение 
является функцией только состояния робота 
.
![\[ {\textbf z}_p = {\textbf z}_p(\textbf x) \]](https://quicklatex.com/cache3/30/ql_1c970924d091282f5a3c442dd3223730_l3.png "Rendered by QuickLaTeX.com")
Состояние робота представляет собой вектор переменных, используемый для описания его текущего состояния (статуса). В случае простого движения на плоскости:
![\[ {\textbf x} = \left(\begin{array}{c}x \\ y \\ \theta \end{array}\right) \]](https://quicklatex.com/cache3/55/ql_52605b2b4f003a60bf7b45a360f1c155_l3.png "Rendered by QuickLaTeX.com")
Это вектор линейных координат 
, 
и угла повора робота .
Измерения, производимые при помощи проприоцептивных датчиков могут зависеть не только от текущего состояния, но и от предыдущих состояний или же от текщей скорости изменения состояния. Например, колесная одометрия дает нам показания, зависящие от разницы между текущим и предыдущим состоянием. Гироскоп выдает показания, зависящие от текущей скорости вращения.
Датчики внешней среды
Без датчиков внешней среды робот движется вслепую. Внешние датчики принимают участие в:
- распознавании мест и объектов, которые уже встречались ранее;
- определении свободного пространства и планирования в нем движения для того, чтобы избежать столкновений с препятствиями;
- взаимодействии с предметами, льдьми и животными;
- создании общего представления об окружающей робота среде.
Измерения, производимые датчиками внешней среды, зависят и от состояния робота 
и от состояния окружающего его мира 
:
![\[ {\textbf z}_0 = {\textbf z}_0({\textbf x}, {\textbf y}) \]](https://quicklatex.com/cache3/5d/ql_d2c338e2704a1ff58a0bca1ed64d705d_l3.png "Rendered by QuickLaTeX.com")
Описать состояние внешнего мира мы можем, например, рядом координат стен, ориентиров.
Состояние может быть либо неопределенным, либо полностью известным.
Вероятностное моделирование датчика
Как и движение робота, измерения которые производят датчики, являются неопределенными. Реальные датчики всегда выдают некоторый разброс значений, измеряют с определенной точностью. В результатах измерений, произведенными тем или иным датчиком всегда присутствует некоторая погрешность.
Мы можем охарактеризовать датчик, построив его математическую модель. Поняв неопределенность, которая присутствует в производимых сенсором измерениях, мы можем построить вероятностную модель измерений. Такая модель будет представлять из себя распределение вероятностей (функцию правдоподобия) вида:
![\[ p({\textbf z}_0 | \textbf x, \textbf y) \]](https://quicklatex.com/cache3/d6/ql_1e1591219f3c83d0fe5cf33dfaea99d6_l3.png "Rendered by QuickLaTeX.com")
Это распределение имеет вид колоколообразной кривой (вид гауссиана).
Функция правдоподобия показывает, какова вероятность эталонного значения 
при получении значения 
. Используя функцию правдоподобия можно оценить неизвестный параметр при известных результатах (когда используется понятие вероятность, мы, наобоорот, используя значение параметра хотим предсказать результат).
Функция правдоподобия полностью описывает работу датчика.
является функцией и переменных измерения 
и эталона 
и может быть построена в виде вероятностной поверхности. Например, для датчика расстояния (дальномера), вероятностная поверхность выглядит следующим образом:
Вероятностная модель дальномера
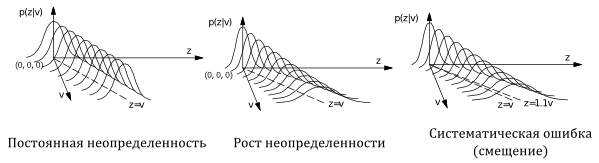
Как же должна выглядеть робастная (устойчивая к шуму) модель датчика?
Чем более пологой является функция правдоподобия, тем больше неопределенности она содержит. Поэтому, чем ярче выражена «пиковость» измерителя, тем меньше неопределенности он содержит в своих показаниях.
Приведу пример. Функция правдоподобия для ультразвукового датчика говорит нам, какова вероятность измерения , полученного датчиком, учитывая, что истинное ожидаемое значение 
.
Устойчивая модель ультразвукового датчика
![\[p(z|m) \propto e^{\frac{-(z-m)^2}{2 \sigma_s^2}} + K\]](https://quicklatex.com/cache3/13/ql_78d8289d16b50f5e682892b34d4d8913_l3.png "Rendered by QuickLaTeX.com")
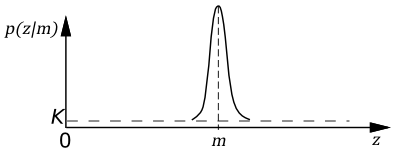
Это распределение имеет форму узкой гауссовой кривой вокруг ожидаемого значения с некоторым постоянным уровнем 
, который отражает фиксированный процент «мусорных измерений».
(11 голосов, средняя оценка: 3,73 из 5)
Загрузка...Еще по этой теме
Описание движения мобильного робота
Самокалибровка при измерениях
Комплект разработчика для камеры RealSense
AlphaGo обыгрывает чемпионов
Первый в мире «умный» 6-осевой датчик ИНС от Fairchild
Дешевый LIDAR для автоматического торможения
LIDAR на чипе: быстрое и дешевое сканирование
Робот телеприсутствия DORA дает невероятное ощущение реальности
Сенсор LIDAR за 100$
Сенсор, который превратит ваш телефон в 3D-сканер
Метки:
Если присутствует внешняя система координат, все это теряет смысл.
Если робот ориентируется не по собственным энкодерам, а например по своему положению относительно конкретной точки, или стенам помещения, показаниям GPS/GlONASS, по звездам и т.п., то погрешности такого рода не будет.