Погрешность, точность и разрешение

Измеряемые величины не могут быть определены абсолютно достоверно. Измерительные инструменты и системы всегда имеют некоторое допустимое отклонение и помехи, которые выражаются степенью неточности. К тому же, необходимо учитывать и особенности конкретных приборов.

В отношении неточности измерений часто используются следующие термины:

Погрешность - ошибка между истинным и измеренным значением
Точность — случайный разброс измеренных значений вокруг их среднего
Разрешение — наименьшая различаемая величина измеренного значения

Часто эти термины путаются. Поэтому здесь я хотел бы подробно рассмотреть вышеуказанные понятия.

Неточность измерения

Неточности измерения могут быть разделены на систематические и случайные измерительные ошибки. Систематические ошибки вызваны отклонениями при усилении и настройкой «нуля» измерительного оборудования. Случайные ошибки вызваны шумом и индуцированными напряжениями и/или токами.

Погрешность и точность

Часто понятия погрешность и точность рассматриваются как синонимы. Однако, эти термины имеют совершенно различные значения. Погрешность показывает, насколько близко измеренное значение к его реальной величине, то есть отклонение между измеренным и фактическим значением. Точность относится к случайному разбросу измеряемых величин.

Когда мы проводим некоторое число измерений до момента стабилизации напряжения или же какого-то другого параметра, то в измеренных значениях будет наблюдаться некоторая вариация. Это вызвано тепловым шумом в измерительной цепи измерительного оборудования и измерительной установки. Ниже, на левом графике показаны эти изменения.

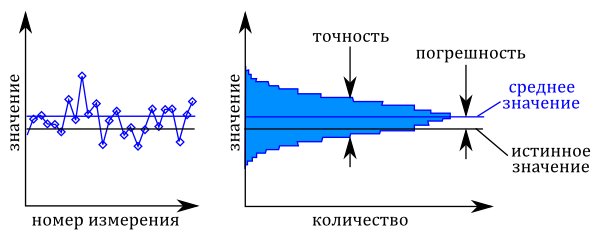
Гистограмма

Измеренные значения могут быть изображены в виде гистограммы, как показано справа на рисунке. Гистограмма показывает, как часто наблюдается измеренное значение. Самая высокая точка на гистограмме, это чаще всего наблюдаемое измеренное значение, в случае симметричного распределения равно среднему значению (изображено синей линии на обоих графиках). Черная линия представляет истинное значение параметра. Разница между средним измеренной величины и истинным значением и является погрешностью. Ширина гистограммы показывает разброс отдельных измерений. Этот разброс измерений называется точностью.

Используйте правильные термины

Погрешность и точность, таким образом, имеют различные значения. Поэтому вполне возможно, что измерение является очень точным, но имеющим погрешность. Или наоборот, с малой погрешностью, но не точное. В общем, измерение считается достоверным, если оно точное, и с малой погрешностью.

Погрешность

Погрешность является индикатором корректности измерения. Из-за того, что в одном измерении точность оказывает влияние на погрешность, то учитывается среднее серии измерений.

Погрешность измерительного прибора обычно задается двумя значениями: погрешностью показания и погрешностью по всей шкале. Эти две характеристики вместе определяют общую погрешность измерения. Эти значения погрешности измерения указываются в процентах или в ppm (parts per million, частей на миллион) относительно действуюшего национального стандарта. 1% соответствует 10000 ppm.

Погрешность приводится для указанных температурных диапазонов и для определенного периода времени после калибровки. Обратите внимание, что в разных диапазонах, возможны, и различные погрешности.

Погрешность показаний

Указание процентного отклонения без дополнительной спецификации также относится к показанию. Допустимые отклонения делителей напряжения, точность усиления и абсолютные отклонения при считывании и оцифровке являются причинами этой погрешности.

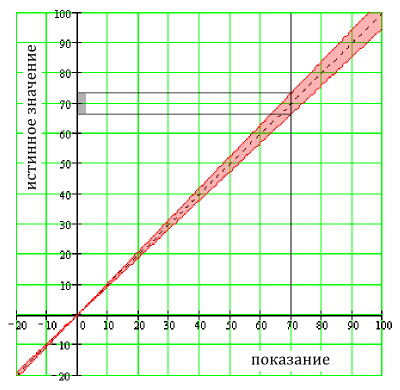
Неточность показаний в 5% для значения 70 В

Вольтметр, который показывает 70.00 В и имеет спецификацию «± 5% от показаний», будет обладать погрешностью в ±3.5 В (5% от 70 В). Фактическое напряжение будет лежать между 66.5 и 73.5 вольтами.

Погрешность по всей шкале

Этот тип погрешности обусловлен ошибками смещения и ошибками линейности усилителей. Для приборов, которые оцифровывают сигналы, присутствует нелинейность преобразования и погрешности АЦП. Эта характеристика относится ко всему используемому диапазону измерений.

Вольтметр может иметь характеристику «3% шкалы». Если во время измерения выбран диапазон 100 В (равный полной шкале), то погрешность составляет 3% от 100 В = 3 В независимо от измеренного напряжения. Если показание в этом диапазоне 70 В, то реальное напряжение лежит между 67 и 73 вольтами.

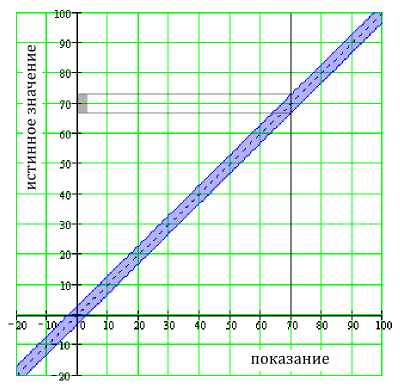
Допустимое отклонение по шкале — Погрешность 3% шкалы в диапазоне 100 В

Из приведенного выше рисунка ясно, что этот тип допустимых отклонений не зависит от показаний. При показании 0 В реальное напряжение лежит между -3 и 3 вольтами.

Погрешность шкалы в цифрах

Часто для цифровых мультиметров приводится погрешность шкалы в разрядах вместо процентного значения.

У цифрового мультиметра с 3½ разрядным дисплеем (диапазон от -1999 до 1999), в спецификации может быть указано «+ 2 цифры». Это означает, что погрешность показания 2 единицы. Например: если выбирается диапазон 20 вольт (± 19.99), то погрешность шкалы составляет ±0.02 В. На дисплее отображается значение 10.00, а фактическое значение будет между 9.98 и 10.02 вольтами.

Вычисление погрешности измерения

Спецификации допустимых отклонений показания и шкалы вместе определяют полную погрешность измерения прибора. Ниже при расчете используются те же значения, что и в приведенных выше примерах:

Точность: ±5% показания (3% шкалы)

Диапазон: 100 В

Показание: 70 В

Полная погрешность измерения вычисляется следующим образом:

$\frac{\%_{reading}}{100\%} =\frac{5\%}{100\%} \cdot 70B = 3.5B$

$\frac{\%_{fullscale}}{100\%} \cdot range = \frac{3\%}{100\%} \cdot 100B = 3B$

$3.5B + 3B = 6.5B$

В этом случае, полная погрешность ±6.5В. Истинное значение лежит между 63.5 и 76.5 вольтами. На рисунке ниже это показано графически.

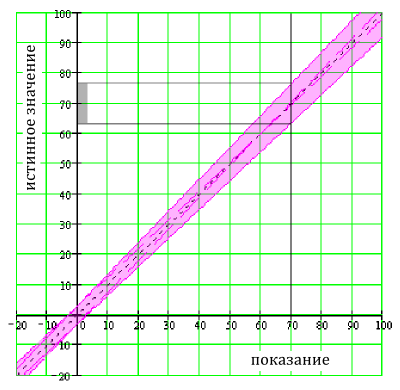
Полное допустимое отклонение — Полная неточность для неточностей показания 5% и 3% шкалы для диапазона 100 В и показания 70 В

Процентная погрешность - это отношение погрешности к показанию. Для нашего случая:

$\frac{uncertainty}{reading} \cdot 100\% = \frac{6.5}{70 B} \cdot 100\% = 9.3\%$

Цифры

Цифровые мультиметры могут иметь спецификацию «± 2.0% показания, + 4 цифры». Это означает, что 4 цифры должны быть добавлены к 2% погрешности показания. В качестве примера снова рассмотрим 3½ разрядный цифровой индикатор. Он показывает 5.00 В для выбранного диапазона 20 В. 2% показания будет означать погрешность в 0,1 В. Добавьте к этому численную погрешность (= 0,04 В). Общая погрешность, следовательно, 0,14 В. Истинное значение должно быть в диапазоне между 4.86 и 5,14 вольтами.

Суммарная погрешность

Зачастую в расчет принимается только погрешность измерительного прибора. Но также, дополнительно следует принимать во внимание погрешности измерительных инструментов, в том случае, если они используются. Вот несколько примеров:

Увеличение погрешности при использовании пробника 1:10

Если в процессе измерений используется щуп 1:10, то необходимо учитывать не только измерительную погрешность прибора. На погрешность также влияет входной импеданс используемого прибора и сопротивление щупа, которые вместе составляют делитель напряжения.

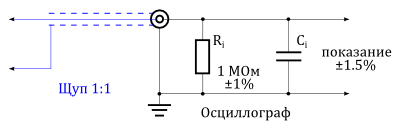
На рисунке выше схематически показан осциллограф с подключенным к нему пробником 1:1. Если мы рассмотрим этот пробник как идеальный (нет сопротивления соединения), то приложенное напряжение передается прямо на вход осциллографа. Погрешность измерения теперь определяется только допустимыми отклонениями аттенюатора, усилителя и цепями, принимающими участие в дальнейшей обработке сигнала и задается производителем прибора. (На погрешность также влияет сопротивление соединения, которое формирует внутреннее сопротивление $R_i$ . Оно включается в заданные допустимые отклонения).

На рисунке ниже показан тот же самый осциллограф, но теперь ко входу подключен щуп 1:10. Этот пробник имеет внутреннее сопротивление соединения $R_p$ и вместе со входным сопротивлением осциллографа $R_i$ образует делитель напряжения. Допустимое отклонение резисторов в делителе напряжения является причиной его собственной погрешности.

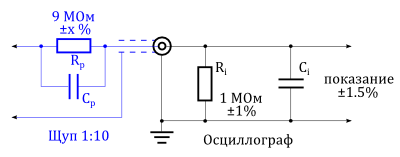
Пробник 1:10, подключенный к осциллографу, вносит дополнительную погрешность

Допустимое отклонение входного сопротивления осциллографа может быть найдено в его спецификации. Допустимое отклонение сопротивления соединения щупа $R_p$ не всегда дано. Тем не менее, погрешность системы заявляется производителем определенного осциллографического пробника для конкретного типа осциллографа. Если щуп используется с другим типом осциллографа, нежели рекомендуемый, то измерительная погрешность становится неопределенной. Этого нужно всегда стараться избегать.

Предположим, что осциллограф имеет допустимое отклонение 1.5% и используется щуп 1:10 с погрешностью в системе 2.5%. Эти две характеристики можно перемножить для получения полной погрешности показания прибора:

$\%_{total}=\left[ 1-\left(1+\frac{\%_{reading}}{100\%}\right)\cdot\left(1+\frac{\%_{system}}{100\%}\right)\right]\cdot 100\%=$

$= \left[\left(1+\frac{1.5\%}{100\%}\right) \cdot \left(1+\frac{2.5\%}{100\%}\right)-1\right] \cdot 100\%=4.037\%$

Здесь $\%_{total}$ — полная погрешность измерительной системы, $\%_{reading}$ — погрешность показания прибора, $\%_{system}$ — погрешность щупа, подключенного к осциллографу, подходящего типа.

Измерения с шунтирующим резистором

Часто при измерениях токов используют внешний шунтирующий резистор. Шунт имеет некоторое допустимое отклонение, которое влияет на измерение.

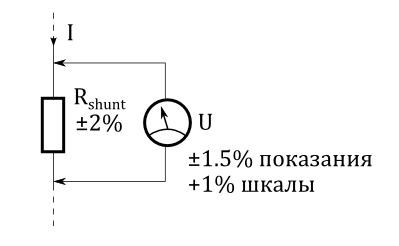
Увеличение погрешности при использовании шунтирующего резистора

Заданное допустимое отклонение шунтирующего резистора влияет на погрешность показания. Для нахождения полной погрешности, допустимое отклонение шунта и погрешность показаний измерительного прибора перемножаются:

$\%_{total}=\left[1-\left(1+\frac{\%_{reading}}{100\%} \right)\right] \cdot 100\%=$

$=\left[\left(1+\frac{1.5\%}{100\%}\right) \cdot \left( 1+\frac{2\%}{100\%}\right) \right] \cdot 100 \% = 3.53\%$

В этом примере, полная погрешность показания равна 3.53%.

Сопротивление шунта зависит от температуры. Значение сопротивления определяется для данной температуры. Температурную зависимость часто выражают в $ppm/ ^\circ C$ .

Для примера вычислим значение сопротивления для температуры окружающей среды $T_{env}=30 ^\circ C$ . Шунт имеет характеристики: $R=100$ Ом $\@ 22 ^\circ C$ (соответственно $R_{nom}$ и $T_{nom}$ ) и температурную зависимость $20 ppm / ^/circ C$ .

$\left[1+(T_{env} - T_{nom}) \cdot \frac{ppm}{1000000} \right] \cdot R_{nom} =$

$= \left[ 1+(30 ^\circ C - 22 ^ \circ C) \cdot \frac{20}{1000000}\right] \cdot 100 \Omega = 100.016 \Omega$

Ток, протекающий через шунт является причиной рассеяния энергии на шунте, что приводит к росту температуры и, следовательно, к изменению значения сопротивления. Изменение значения сопротивления при протекании тока зависит от нескольких факторов. Для проведения очень точного измерения, необходимо откалибровать шунт на дрейф сопротивления и условия окружающей среды при которых проводятся измерения.

Точность

Термин точность используется для выражения случайности измерительной ошибки. Случайная природа отклонений измеряемых значений в большинстве случае имеет тепловую природу. Из-за случайной природы этого шума не возможно получить абсолютную ошибку. Точность дается только вероятностью того, что измеряемая величина лежит в некоторых пределах.

Распределение Гаусса

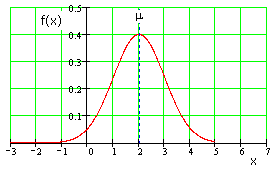
Тепловой шум имеет гауссово, или, как еще говорят, нормальное распределение. Оно описывается следующим выражением:

$f(x)=\frac{1}{\sigma \sqrt{2 \cdot \pi}} \cdot \exp{\left[\frac{-(x-\mu)^2}{2 \cdot \sigma^2}\right]}$

Здесь $\mu$ — среднее значение, $\sigma$ показывает дисперсию и соответствует RMS-значению шумового сигнала. Функция дает кривую распределения вероятностей, как показано на рисунке ниже, где среднее значение $\mu=2$ и эффективная амплитуда шума $\sigma=1$ .

Распределение вероятностей с $\mu=2$ и $\sigma=1$

В таблице указаны шансы получения значений в заданных пределах.

Граница	Шанс
0.5·σ	38.3 %
0.674·σ	50.0 %
1·σ	68.3 %
2·σ	95.4 %
3·σ	99.7 %

Как видно, вероятность того, что измеренное значение лежит в диапазоне ± $3 \sigma$ равна $99.7\%$ .

Повышение точности

Точность может быть улучшена передискретизацией (изменением частоты дискретизации) или фильтрацией. Отдельные измерения усредняются, поэтому шум значительно снижается. Также снижается разброс измеренных значений. Используя передискретизацию или фильтрацию необходимо учитывать, что это может привести к снижению пропускной способности.

Разрешение

Разрешением, или, как еще говорят, разрешающей способностью измерительной системы является наименьшая различимая измеряемая величина. Определение разрешения прибора не относится к точности измерения.

Цифровые измерительные системы

Цифровая система преобразует аналоговый сигнал в цифровой эквивалент посредством аналого-цифрового преобразователя. Разница между двумя значениями, то есть разрешение, всегда равно одному биту. Или, в случае с цифровым мультиметром, это одна цифра.

Возможно также выразить разрешение через другие единицы, а не биты. В качестве примера рассмотрим цифровой осциллограф, имеющий 8-битный АЦП. Чувствительность по вертикали установлена в 100 мВ/дел и число делений равно 8, полный диапазон, таким образом, равен 800 мВ. 8 бит представляются 2⁸=256 различными значениями. Разрешение в вольтах тогда равно 800 мВ / 256 = 3125 мВ.

Аналоговые измерительные системы

В случае аналогового прибора, где измеряемая величина отображается механическим способом, как в стрелочном приборе, сложно получить точное число для разрешения. Во-первых, разрешение ограничено механическим гистерезисом, причиной которого является трение механизма стрелки. С другой стороны, разрешение определяется наблюдателем, делающем свою субъективную оценку.

[add_ratings]

8 thoughts on “Погрешность, точность и разрешение”

Виталий:
10.07.2015 в 20:39
Андрей, спасибо за статью!
А каким(и), если не секрет, вы пользуетесь мультиметром(ми) и почему выбор пал на них?
Ответить
1. Андрей Антонов:
  11.07.2015 в 18:21
  Виталий, здравствуйте. Я никакими секретными приборами не пользуюсь 🙂 Мультиметр у меня UNI-T UT61E. Высокая точность, низкая погрешность, измерения TrueRMS, интерфейс с компьютером (правда, RS-232, но с переходником USB — RS-232 — это уже не проблема). Хороший производитель (UNI-T производит для Fluke), цена очень даже конкурентоспособная. Из недостатков, на мой взляд, только отсутствие отдельной кнопки включения/выключения питания (чтобы выключить нужно селектор режимов крутить в положение OFF, кнопка ВКЛ/ВЫКЛ была бы поудобнее). Покупал здесь. Если нужна еще большая точность и USB-интерфейс можете посмотреть серию UT-71. Там вообще — полный фарш, как говорится. Я множество различных моделей рассматривал (в том числе и настольных) в качестве альтернативы — UT61E мне больше всех приглянулся (возможно, цена тут сыграла главную роль).
  Ответить
  1. Виталий:
    11.07.2015 в 19:53
    Спасибо за совет!
    В данном ценовом сегменте конкурентов по ттх и близко не видно )
    Прицелился и на Brymen BM257s (BM869s вообще мечта, но просто для моих хобби-задач это перебор).
    Brymen, вдруг вам будет интересно, тайваньская компания. Вообще они оставались в тени, т.к. давно работают как ОЕМ для других марок, но некоторое время назад вышли на розничный рынок. Интересный девайс по цене/качеству.
    Буду думать.
    Ответить
Юрий:
27.03.2016 в 19:45
Разрешение и точность — идентичные понятия, не надо выдумывать.
Ответить
1. Андрей Антонов:
  28.03.2016 в 01:40
  Юрий, я же написал
  Термин точность используется для выражения случайности измерительной ошибки. Случайная природа отклонений измеряемых значений, в большинстве случае имеет тепловую природу.
  Разрешение измерительного прибора — это систематическая (не случайная ошибка). В чем, по Вашему мнению, идентичность?
  Ответить
  1. Василий Козлов:
    22.06.2016 в 06:33
    Погрешность и точность это антиподы. Если погрешность показывает степень отклонения измеренного значения от истинного, то точность показывает степень приближения к истинному. И не надо приплетать сюда случайную и систематическую составляющие погрешности. Это же касается и разрешения. О котором автор пишет, что оно не характеризует точность средства измерений, и в то же время заявляет, что «Разрешение измерительного прибора — это систематическая (не случайная ошибка)». Разрешение это изменение измеряемой величины между ,скажем, соседними делениями, которое может различить оператор, без количественной оценки.
    Ответить
Андрей:
02.02.2021 в 08:43
А почему все цифры в статье написаны не по русски?
Для примера 70.00
70•00=0, а скорее всего должно быть 70,00
Ответить
Андрей:
25.02.2022 в 18:31
К сожалению ни одна формула не отображается. Лишь сообщения типа:
*** QuickLaTeX cannot compile formula:
\sigma=1
*** Error message:
Cannot connect to QuickLaTeX server: SSL certificate problem: certificate has expired
Please make sure your server/PHP settings allow HTTP requests to external resources («allow_url_fopen», etc.)
These links might help in finding solution:
wordpress.org/extend/plugins/core-control/
wordpress.org/support/top...ess-3?replies=37
Ответить