Часто в электронных схемах требуется сгенерировать разные типы сигналов, имеющих различные частоты и формы, такие как меандры, прямоугольные, треугольные, пилообразные сигналы и различные импульсы.
Эти сигналы различной формы могут использоваться в качестве сигналов синхронизации, тактирующих сигналов или в качестве запускающих синхроимпульсов. В первую очередь необходимо понять основные характеристики, описывающие электрические сигналы.
С технической точки зрения, электрические сигналы являются визуальным представлением изменения напряжения или тока с течением времени. То есть, фактически — это график изменения напряжения и тока, где по горизонтальной оси мы откладываем время, а по вертикальной оси — значения напряжения или тока в этот момент времени. Существует множество различных типов электрических сигналов, но в целом, все они могут быть разбиты на две основные группы.
- Однополярные сигналы - это электрические сигналы, которые всегда положительные или всегда отрицательные, не пересекающие горизонтальную ось. К однонаправленным сигналам относятся меандр, тактовые импульсы и запускающие импульсы.
- Двухполярные сигналы - эти электрические сигналы также называют чередующимися сигналами, так как они чередуют положительные значения с отрицательными, постоянно пересекая нулевое значение. Двухполярные сигналы имеют периодическое изменение знака своей амплитуды. Наиболее распространенным из двунаправленных сигналов, является синусоидальный.
Будучи однонаправленными, двунаправленными, симметричными, несимметричными, простыми или сложными, все электрические сигналы имеют три общие характеристики:
- Период — это отрезок времени, через который сигнал начинает повторяться. Это временное значение также называют временем периода для синусоид или шириной импульса для меандров и обозначают буквой T.
- Частота - это число раз, которое сигнал повторяет сам себя за период времени равный 1 секунде. Частота является величиной, обратной периоду времени, (
 ). Единицей измерения частоты является Герц (Гц). Частотой в 1Гц, обладает сигнал, повторяющий 1 раз за 1 cекунду.
). Единицей измерения частоты является Герц (Гц). Частотой в 1Гц, обладает сигнал, повторяющий 1 раз за 1 cекунду. - Амплитуда — это величина изменения сигнала. Измеряется в Вольтах (В) или Амперах (А), в зависимости от того, какую временную зависимость (напряжения или тока) мы используем.
Периодические сигналы
Периодические сигналы являются самыми распространенными, поскольку включают в себя синусоиды. Переменный ток в розетке дома представляет из себя синусоиду, плавно изменяющуюся с течением времени с частотой 50Гц.
Время, которое проходит между отдельными повторениями цикла синусоиды называется ее периодом. Другими словами, это время, необходимое для того, чтобы сигнал начал повторяться.
Период может изменяться от долей секунды до тысяч секунд, так как он связан с его частотой. Например, синусоидальный сигнал, которому требуется 1 секунда для совершения полного цикла, имеет период равный одной секунде. Аналогично, для синусоидального сигнала, которому требуется 5 секунд для совершения полного цикла, имеет период равный 5 секундам, и так далее.
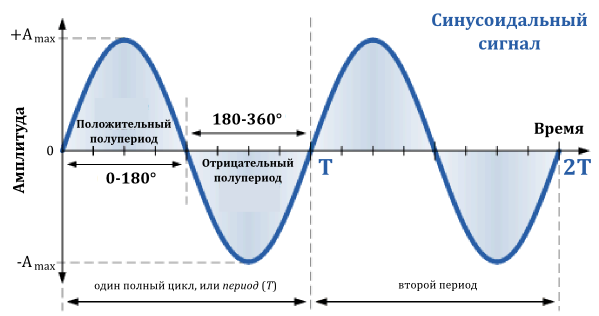
Итак, отрезок времени, который требуется для сигнала, чтобы завершить полный цикл своего изменения, прежде чем он вновь повторится, называется периодом сигнала и измеряется в секундах. Мы можем выразить сигнал в виде числа периодов T в секунду, как показано на рисунке ниже.
Синусоидальный сигнал
Время периода часто измеряется в секундах ( с ), миллисекундах (мс) и микросекундах (мкс).
Для синусоидальной формы волны, время периода сигнала также можно выражать в градусах, либо в радианах, учитывая, что один полный цикл равен 360° (Т = 360°), или, если в радианах, то ![]() (T =
(T = ![]() ).
).
Период и частота математически являются обратными друг другу величинами. С уменьшением времени периода сигнала, его частота увеличивается и наоборот.
Соотношения между периодом сигнала и его частотой:
![]() Гц
Гц
![]() c
c
Один герц в точности равен одному циклу в секунду, но один герц является очень маленькой величиной, поэтому часто можно встретить префиксы, обозначающие порядок величины сигнала, такие как кГц, МГц, ГГц и даже ТГц
| Префикс | Определение | Запись | Период |
| Кило | тысяча | кГц | 1 мс |
| Мега | миллион | МГц | 1 мкс |
| Гига | миллиард | ГГц | 1 нс |
| Тера | триллион | ТГц | 1 пс |
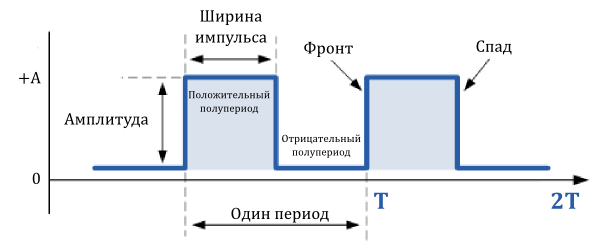
Меандр
Меандры широко используются в электронных схемах для тактирования и сигналов синхронизации, так как они имеют симметричную прямоугольную форму волны с равной продолжительностью полупериодов. Практически все цифровые логические схемы используют сигналы в виде меандра на своих входах и выходах.
Так как форма меандра симметрична, и каждая половина цикла одинакова, то длительность положительной части импульса равна промежутку времени, когда импульс отрицателен (нулевой). Для меандров, используемых в качестве тактирующих сигналов в цифровых схемах, длительность положительного импульса называется временем заполнения периода.
Для меандра, время заполнения ![]() равно половине периода сигнала. Так как частота равна обратной величине периода, (1/T), то частота меандра:
равно половине периода сигнала. Так как частота равна обратной величине периода, (1/T), то частота меандра:
![]()
Например, для сигнала с временем заполнения равным 10 мс, его частота равна:
![]() Гц
Гц
Меандры используются в цифровых системах для представления уровня логической «1» большими значениями его амплитуды и уровня логического «0» маленькими значениями амплитуды.
Если время заполнения, не равно 50% от длительности его периода, то такой сигнал уже представялет более общий случай и называется прямоугольным сигналом. В случае, или если время положительной части периода сигнала мало, то такой сигнал, является импульсом.
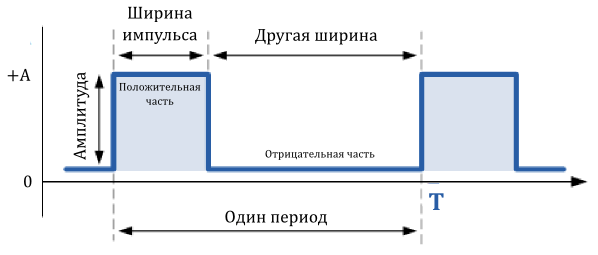
Прямоугольный сигнал
Прямоугольные сигналы отличаются от меандров тем, что длительности положительной и отрицательной частей периода не равны между собой. Прямоугольные сигналы поэтому классифицируются как несимметричные сигналы.
В данном случае я изобразил сигнал, принимающий только положительные значения, хотя, в общем случае, отрицательные значения сигнала могут быть значительно ниже нулевой отметки.
На изображенном примере, длительность положительного импульса больше, чем длительность отрицательного, хотя, это и не обязательно. Главное, чтобы форма сигнала была прямоугольной.
Отношение периода повторения сигнала ![]() , к длительности положительного импульса
, к длительности положительного импульса ![]() , называют скважностью:
, называют скважностью:
![]()
Величину обратную скважности называют коэффициентом заполнения (duty cycle):
![]()
Пример расчета
Пусть имеется прямоугольный сигнал с импульсом длительностью 10мс и коэффициентом заполнения 25%. Необходимо найти частоту этого сигнала.
Коэффициент заполнения равен 25% или ¼, и совпадает с шириной импульса, которая составляет 10мс. Таким образом, период сигнала должен быть равен: 10мс (25%) + 30мс (75%) = 40мс (100%).
Гц
Прямоугольные сигналы могут использоваться для регулирования количества энергии, отдаваемой в нагрузку, такую, например, как лампа или двигатель, изменением скважности сигнала. Чем выше коэффициент заполнения, тем больше среднее количество энергии должно быть отдано в нагрузку, и, соответственно, меньший коэффициент заполнения, означает меньшее среднее количество энергии, отдаваемое в нагрузку. Отличным примером этого является использование широтно-импульсной модуляции в регуляторах скорости. Термин широтно-импульсная модуляция (ШИМ) буквально и означает «изменение ширины импульса».
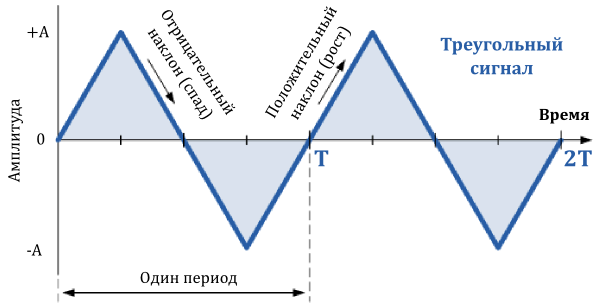
Треугольные сигналы
Треугольные сигналы, как правило, это двунаправленные несинусоидальные сигналы, которые колеблются между положительным и отрицательным пиковыми значениями. Треугольный сигнал представляет собой относительно медленно линейно растущее и падающее напряжение с постоянной частотой. Скорость, с которой напряжение изменяет свое направление равна для обоих половинок периода, как показано ниже.
Как правило, для треугольных сигналов, продолжительность роста сигнала, равна продолжительности его спада, давая тем самым 50% коэффициент заполнения. Задав амплитуду и частоту сигнала, мы можем определить среднее значение его амплитуды.
В случае несимметричной треугольной формы сигнала, которую мы можем получить изменением скорости роста и спада на различные величины, мы имеем еще один тип сигнала известный под названием пилообразный сигнал.
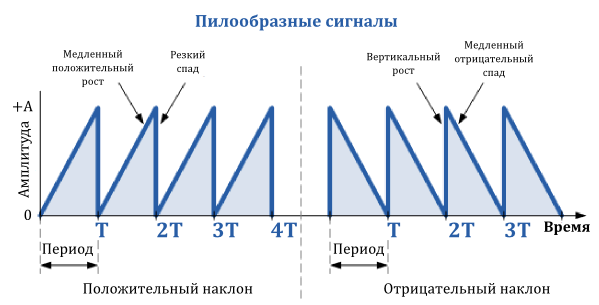
Пилообразный сигнал
Пилообразный сигнал — это еще один тип периодического сигнала. Как следует из названия, форма такого сигнала напоминает зубья пилы. Пилообразный сигнал может иметь зеркальное отражение самого себя, имея либо медленный рост, но очень крутой спад, или чрезвычайно крутой, почти вертикальный рост и медленный спад.
Пилообразный сигнал с медленным ростом является более распространенным из двух типов сигналов, являющийся, практически, идеально линейным. Пилообразный сигнал генерируется большинством функциональных генераторов и состоит из основной частоты (f) и четных гармоник. Это означает, с практической точки зрения, что он богат гармониками, и в случае, например, с музыкальными синтезаторами, для музыкантов дает качественный звук без искажений.
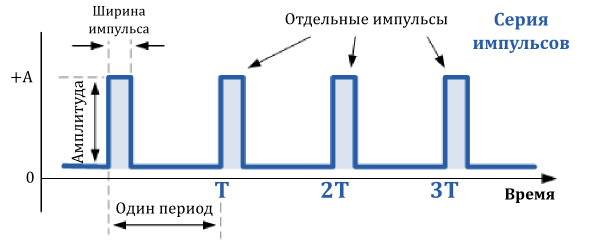
Импульсы и запускающие сигналы (триггеры)
Хотя, технически, запускающие сигналы и импульсы два отдельных типа сигналов, но отличия между ними незначительны. Запускающий сигнал — это всего лишь очень узкий импульс. Разница в том, что триггер может быть как положительной, так и отрицательной полярности, тогда как импульс только положительным.
Форма импульса, или серии импульсов, как их чаще называют, является одним из видов несинусоидальной формы сигналов, похожей на прямоугольный сигнал. Разница в том, что импульсный сигнал определяется часто только коэффициентом заполнения. Для запускающего сигнала положительная часть сигнала очень короткая с резкими ростом и спадом и ее длительностью, по сравнению с периодом, можно пренебречь.
Очень короткие импульсы и запускающие сигналы предназначены для управления моментами времени, в которые происходят, например, запуск таймера, счетчика, переключение логических триггеров а также для управления тиристорами, симисторами и другими силовыми полупроводниковыми приборами.
Я рассмотрел здесь только основные виды электрических сигналов. Остальные типы сигналов, обычно, получают их комбинацией или модуляцией (изменением параметров, используя другой сигнал), например:
- Амплитудно-модулированный сигнал
- Частотно-модулированный сигнал
- Фазо-модулированный сигнал
- Фазо-частотно-модулированный сигнал
- Фазо-кодо-манипулированный сигнал
Подробно я вернусь к ним в своих последующих публикациях.
[add_ratings]









Исправьте: для меандра первая формула не соответствует картинке!
частота = 1 / Т = 1 / (Тимпильса + Тпаузы)
Спасибо. Исправил обозначение.
В формулах расчета частоты (50 и 25 Гц) к миллисекундам в знаменателе добавьте 10^-3, иначе из-за неправильной размерности получается ошибка в арифметике.
Добавил, спасибо. Там нужно было написать мс, но есть у меня техническая проблема с написанием кириллицей в формулах.
Описание хорошее, но почему нигде нет представления в математической форме? Например, синусоиду можно представить как S (t)=A0*sin (w*t). А как представлять остальные сигналы (к примеру трапецевидный)? В ряде случаев это необходимо, но в литературе это игнорят, будто начинающие люди такие вундеркинды и у них в голове прошивка радиогения. Будьте любезны, объясните пожалуйста.
Спасибо,Очень познавательная статья,
Фундаментальной наукой для специальности Целостность сигналов по большей части является теория электромагнетизма . Теория электромагнетизма опирается на уравнения Максвелла , записанные им в 1873 году. При изучении целостности сигналов чаще всего пользуются интуитивно понятной дифференциальной формой уравнений. Однако, при необходимости, может быть использована и интегральная форма уравнений.
спасибо за статью
Если в первом примере по прямоугольным импульсам частота равна 1/(40*10^-3) = 1/(4*10^-4) = 10^4*¼ = 10^4 * 0,25 = 2500 Гц, а не 25Гц или я ошибся?
Как отобразить все эти сигналы графиками в Exel?
Как решить задачу . Определить частоту следования импульсов если их период равен 200 мкс