Третье измерение в Processing

Это может показаться менее интригующим, чем разговор о четвертом или пятом измерениях, я уже не говорю про десяток измерений в теории струн, но эта тема многих ставит в тупик при попадании в мир компьютерной графики. Давайте внимательно посмотрим на то, что же имеется в виду, когда речь заходит о 3D.

Мы с вами живем в трехмерном мире (по-крайней мере, мы так думаем), хотя наши экраны и различные интерфейсы традиционно являются двухмерными. С появлением 3D сканеров реального времени, таких как сенсор Kinect, это ограничение осталось позади. Мы можем взаимодействовать с компьютером, используя три измерения физического пространства.

Наши экраны пока еще двухмерные, поэтому для представления трех пространственных измерений на дисплее требуется использовать некоторые математические преобразования, которые не обязательно заново изобретать, потому что умные люди все уже давно придумали и реализовали. Processing поддерживает работу с 3D и имеет два различных 3D визуализатора (или как еще их называют — рендера), носящих названия P3D и OpenGL. Я остановлюсь на OpenGL, потому что из этих двух, он более мощный.

Processing в 3D

Давайте создадим простенький скетч для демонстрации работы в трех измерениях.

Существует два 3D-примитива, которые уже реализованы в Processing — это box () и sphere (). Мы собираемся нарисовать на экране трехмерный ящик.

Для этого, прежде всего, необходимо импортировать встроенную библиотеку OpenGL в наш скетч. Мы указываем в качестве рендера OPENGL в функции size (), находящейся внутри setup (). Затем в циклически выполняющейся функции draw (), установим белым цвет фона, переместимся в центр экрана и изобразим куб со сторонами в 200 единиц.

import processing.opengl.*;

void setup()
{
  size(800, 600, OPENGL);
}
void draw()
{
  background(255);
  noFill();
  translate(width/2,height/2);
  box(200);
}

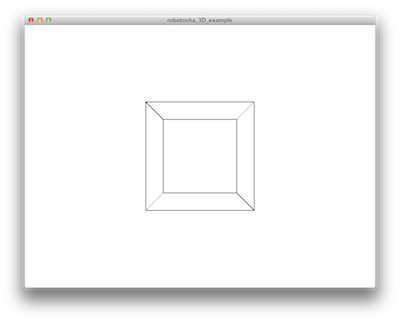
Результат выполнения этой простенькой программы показан на скриншоте.

Функция translate (), которую мы использовали в этом примере является одной из функций Processing для выполнения преобразований. Общим для этих функций является то, что они влияют на текущую матрицу преобразования.

Матрица преобразований

Матрица преобразования является системой отсчета, которую Processing использует для вывода объектов на экран. Если вы не изменяли матрицу преобразования, то началом координат будет являться верхний левый угол экрана, ось х указывает направо, а ось y — вниз.

Если вы рисуете прямоугольник на экране, то вы можете в параметрах функции rect (x, y, width, height) указать координаты х и у его центра. Но если вы хотите нарисовать коробку (параллелепипед), то функция box (width, height, depth) не имеет параметров позиции. Можно даже указывать просто размер стороны для куба в виде box (size).

Так что, если вы хотите нарисовать параллелепипед в положении отличном от глобальной системы координат, необходимо изменить систему отсчета на место и ориентацию в которой вы хотели бы видеть коробку. Таким образом, когда отобразится окно, параллелепипед появится в нужном месте. Это будет сделано используя матрицу преобразований.

Измените код на следующий:

import processing.opengl.*;

void setup()
{
  size(800, 600, OPENGL);
}
void draw()
{
  background(255);
  noFill();
  translate(mouseX,mouseY);
  rotate(45);
  box(200);
}

и посмотрите, что он делает на экране

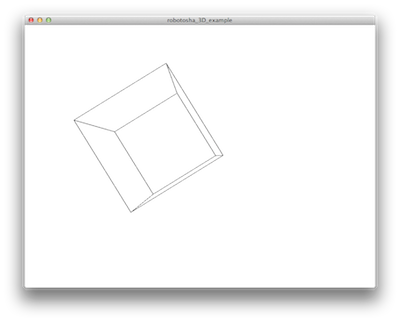
Управление параллелепипедом происходит изменением положения мыши.

Если вы хотите изменить матрицу преобразования для некоторых операций, а затем вернуть ее в прежнее состояние, вы можете использовать методы pushMatrix () и popMatrix (). Первый метод будет помещать текущую матрицу в матричный стек, из которого вы можете восстановить ее, используя popMatrix (). Итак, мы можем сохранить матрицу, используя pushMatrix (), выполнить некоторые преобразования и отобразить некоторые объекты, а затем восстановить предыдущую матрицу, используя popMatrix () и продолжить рисование объектов в предыдущей системе координат. Это проиллюстрировано с помощью следующего кода

import processing.opengl.*;

void setup()
{
  size(800, 600, OPENGL);
}

void draw()
{
  background(255);
  noFill();

  pushMatrix();
  translate(mouseX,mouseY);
  rotate(45);
  box(200);
  translate(300,0);
  box(50);
  popMatrix();
  translate(200,200);
  box(100);
}

В результате получится

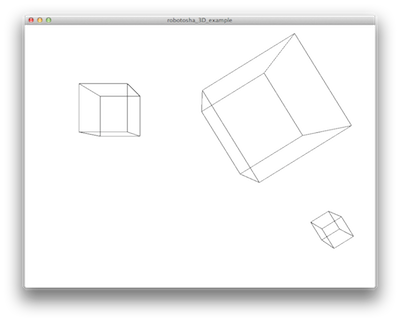
Если вы поиграетесь с этой программкой некоторое время, то поймете, что эти два куба следуют за мышью и поворачиваются на 45 градусов, в то время, как третий куб все время остается на своем месте. Проанализируйте код, и вы поймете, почему это происходит. Во-первых, мы помещаем матрицу в стек, а затем перемещаемся в точку, определяемую координатами мыши, поворачиваем на угол 45 градусов и отображаем большой куб. Затем мы снова перемещаем матрицу по оси х, но поскольку матрица уже перемещена и повернута, это привело к движению по диагонали, так что второй куб отображается повернутым в правом нижнем углу от первого.

Затем мы извлекаем матрицу из стека, тем самым вернувшись к исходной системе координат. Затем мы перемещаем восстановленную матрицу на определенное расстояние по x и y и рисуем третью коробку, которая не будет перемещаться при помощи мыши. Последнее преобразование не аккумулируется, так как каждый раз, когда у нас запускается новый цикл draw (), матрица сбрасывается.

[add_ratings]