Задачи машинного обучения — ищем закономерности и предсказываем будущее

Продолжаю публикацию материалов, посвященных алгоритмам, применяемым в робототехнике. В предыдущей статье я рассмотрел проблемы, которые могут встретиться при обработке различных данных, используемых роботами. Я также упомянул, что для решения этих проблем мы можем использовать алгоритмы машинного обучения либо инструменты вероятностного рассуждения.  Сегодня речь пойдет о машинном обучении.

Задача регрессии

Используя регрессионный анализ мы можем найти зависимость одной переменной от другой путем «подгонки» имеющихся опытных данных некоторой функцией. Например, робот-футболист фиксирует положение мяча, через определенные моменты времени, то есть мы имеем некоторый дискретный набор значений. При этом, наши данные включают некоторую «шумовую» составляющую (этот шум может вносить наш датчик, например, видеокамера робота). И задачей является определить траекторию движения мяча и, зная ее, предсказать его положение в некоторый момент времени в будущем, на основе чего уже сформировать стратегию поведения робота.

Это задача решается методами обучения с учителем.

Задачи, которые мы пытаемся решить:

• Найти лучшую кривую(функцию) для подгонки уже имеющихся данных;
• Предсказать значение функции для новой точки данных (если имеющиеся данные представляют из себя временной ряд, как в случае с мячом, то, по-сути, нам нужно предсказать где же в будущем окажется этот мяч)

Более формально:

• Пусть X набор данных (в нашем случае — некоторые точки на оси времени)
• Предположим, что y - соответствующие им значения (координаты мяча)
• Необходимо найти такую функцию f что f (X) ≈ y

точки во времени X → f (X) → координаты мяча y

• Используя найденную функцию f, найти значение y для нового X (определить положение мяча в некоторый момент в будущем)
• Оценить качество полученного результата (насколько близко оказалось фактическое положение мяча по-отношению к предсказанному)

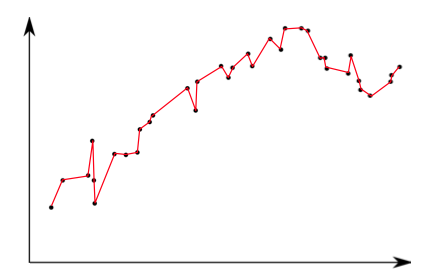
Выбор функции f (X) является достаточно сложной задачей, и вот почему. Если представить нашу функцию, которую называю целевой в виде полинома, то увеличивая степень этого полинома, мы сможем все лучше и лучше описать наши данные, полученные в прошлом. На картинке я показал пример подгонки точек данных линейной, квадратичной и кубическими функциями.

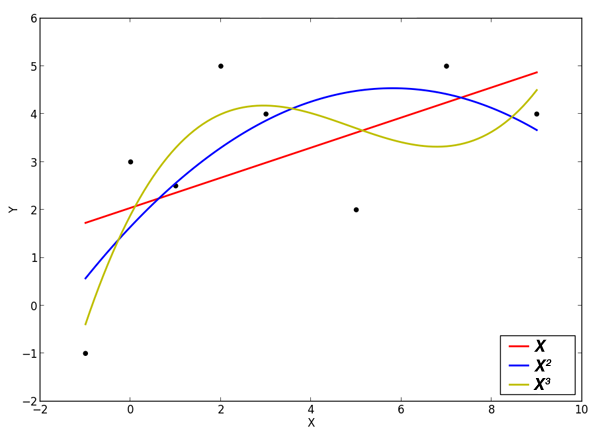
Увеличивая степень полинома, в какой-то момент можно достичь того, что все наши данные попадут на кривую, описываемую функцией f (X).

В этом случае возникает две проблемы. Первая — мы получили сложную модель (функцию). Вторая — полученная модель плохо обобщает, то есть она очень хорошо описывает данные, полученные в прошлом, но при использовании ее в предсказании, она, как правило, дает достаточно большую ошибку.   Это, так называемая, проблема «переподгонки данных» или «переобучения».

Очень часто при решении регрессионных задач применяется линейная регрессия, когда в качестве функции, которой мы пытаемся подогнать наши данные выступает обычная прямая (линейная функция).

Задача кластеризации

Следующая группа задач, которую позволяют решать алгоритмы машинного обучения — это задачи кластеризации.

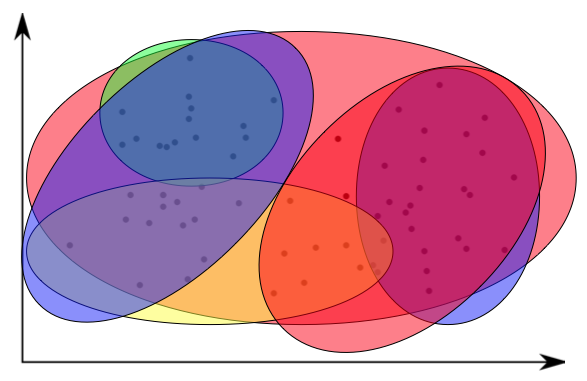
Это пример обучения без учителя.

Мы пытаемся:

• Выделить некие общности (кластеры) в имеющихся данных, другими словами, хоти сгруппировать данные в классы, которые нам изначально неизвестны.
• Предсказать к какому из полученных классов относится новая точка данных

Более формально:

• Пусть X — набор точек данных;
• Необходимо выделить набор классов K
• Найти связь между X и k.

Вариантов, как объединять имеющиеся данные может быть множество (см. рисунок выше).

Для решения этой задачи часто применяют алгоритм k-means (k-средних) и алгоритм для нахождения оценок максимального правдоподобия, или EM-алгоритм (Expectation Maximization algorithm).

Задача классификации

Представьте, что у нас есть набор данных и мы может отнести точку данных к тому или иному классу (например «свой» - «чужой»). Теперь у нас появляется новое значение и нам нужно определить «свой» это или «чужой». Задачей алгоритма будет найти какие же именно значения позволяют относить данные к тому или иному класcу.

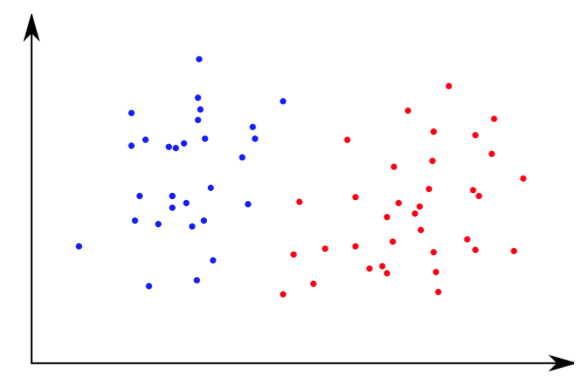
Нам нужно:

• Сгруппировать точки данных в известные классы
• Предсказать класс для новой точки данных

Формулировка:

• Пусть X - набор точек данных
• Пусть k — соответсвующий им класс
• Необходимо найти связь между X и k
• Найти k для нового X
• Оценить результат

Эта задача, как и задача регрессии решается методами обучения с учителем, так как нам известны целевые значения (или результаты испытаний).

Для решения этой задачи часто примяются алгоритм под названием «Машины опорных векторов» (SVM — Support Vector Machines), а также анализ главных компонент (PCA — Principal Components Analysis)

Оценка результатов обучения

Для оценки алгоритмов:

• Сравнивают различные модели

В случае регрессии мы можем сравнивать модели, использующие различные базисные функции, в случае классификации это могут быть различные формы кривых, определяющих классы

• Производят перекрестную проверку (cross-validation)

1. Выбрать часть имеющихся данных (так называемое тренировочное множество)
2. Оптимизировать модель на этих данных
3. Взять другой набор данных, называемый тестовым множеством
4. Оценить результаты работы модели уже на тестовом множестве
5. Повторить пункты 1-4 несколько раз
6. Если ошибка модели не сильно отличается в зависимости от выбранного множества, значит, как говорят статистики, модель является статистически значимой

В следующей публикации, посвященной алгоритмам, используемым в робототехнике я планирую рассказать про вероятностное рассуждение.

[add_ratings]